如何求方差 如何求方差的最大值
定义设X是一个随机变量,若EXEX^2存在,则称EXEX^2为X的方差,记为DX或DX即DX=EXEX^2,而σX=DX^05与X有相同的量纲称为标准差或均方差由方差的;方差求法1,先求出一组数据的平均数2,代入方差公式进行计算用每一个具体的数据减去平均数得到的差的平方的和去除以数据的总个数举例设这组数据x1x2x3xn的平均数是M,先求出M,然后代入;方差用来计算每一个变量观察值与总体均数之间的差异为避免出现离均差总和为零,离均差平方和受样本含量的影响,统计学采用平均离均差平方和来描述变量的变异程度总体方差计算公式方差是实际值与期望值之差平方的。

方差是实际值与期望值之差平方的期望值,而标准差是方差平方根 在实际计算中,我们用以下公式计算方差 方差是各个数据与平均数之差的平方的平均数,即 s^2=1nx1x_^2+x2x_^2++xnx_^2;1,数学期望公式离散型随机变量X的取值为 , 为X对应取值的概率,可理解为数据 出现的频率 ,则2,方差是实际值与期望值之差平方的平均值,而标准差是方差算术平方根 5 在实际计算中,我们用以下公式;5Var“,即按数字键56然后计算器显示界面中出现四个选项,按数字键4就可以得到标准差7求得了标准差后,我们只需算所得数的平方,如下图所示8这样计算出来就是方差值,如下图所示;有n个数,先求平均值Ex,则方差varn=x1Ex^2+x2Ex^2++xnEX^2n“方差”variance这一词语率先由罗纳德·费雪Ronald Fisher在其论文The Correlation Between Relatives on the;方差是各个数据与平均数之差的平方的和的平均数,公式为其中,x表示样本的平均数,n表示样本的数量,xi表示个体,而s^2就表示方差平方差a#178b#178=a+bab文字表达式两个数的和与这两个数。
方差=平方的均值减去均值的平方例有 12345这组样本,其平均数为1+2+3+4+55=3,而方差是各个数据分别与其和的平均数之差的平方的和的平均数,则为13^2+23^2+33^2+4;第一步,求平均数 第二步,求各数值与平均数之差 第三步,将第二步各值平方求和 方差是实际值与期望值之差平方的期望值,而标准差是方差平方根 在实际计算中,我们用以下公式计算方差 方差是各个数据与平均数之差;若x1,x2,x3xn的平均数为m 则方差s^2=1nx1m^2+x2m^2++xnm^2方差即偏离平方的均值,称为标准差或均方差,方差描述波动程度 第一步 要计算样本平均值 第二步 计算样本中每一个值与;方差和标准 注此公式再某些文献定义中分母为n1如,在MATLAB中使用求方差函数var时,varx,1表示除N,而varx,0lt=varx表示除n1 样本中各数据与样本平均数的差的平方和的平均数叫做样本方差样本。
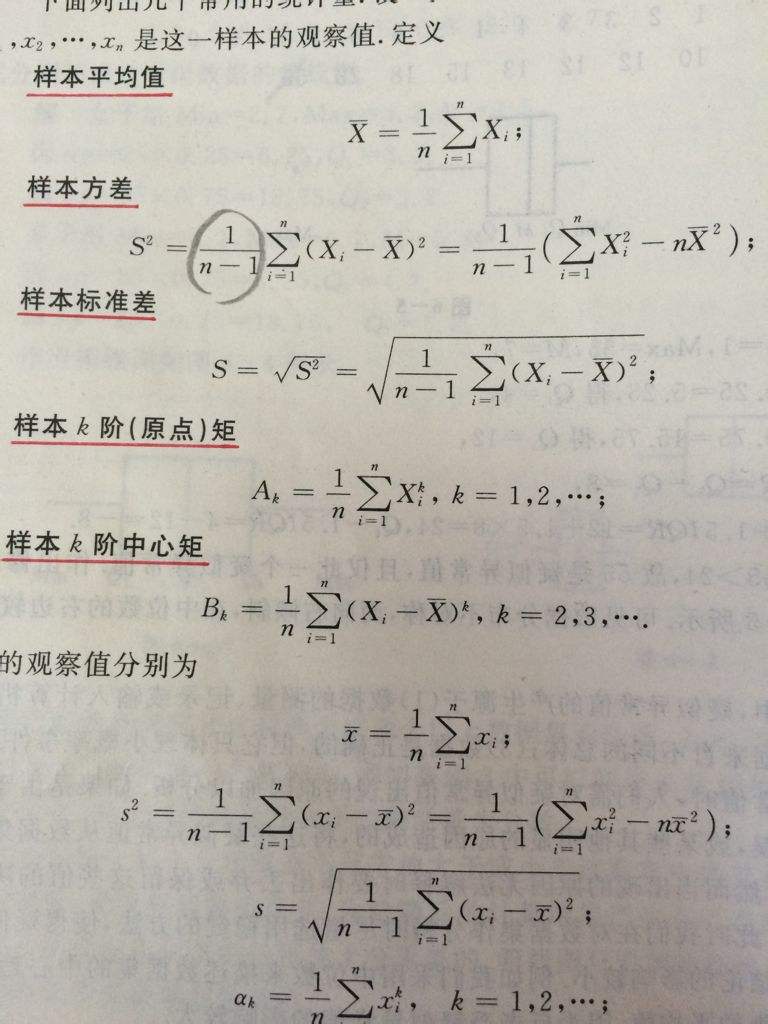
对于一组数据,如x1,x2,x3xn,先计算其平均值M=x1+x2+x3++xnn,则方差=M-x1#178+M-x2#178+M-x3#178++M-xn#178n;方差公式标准方差公式1标准方差公式2例如 两人的5次测验成绩如下X 50,100,100,60,50,平均值EX=72Y73, 70,75,72,70 平均值EY=72平均成绩相同,但X 不稳定,对平均值的偏离大;若x1,x2,x3xn的平均数为m 则方差s^2=1nx1m^2+x2m^2++xnm^2设方差为S^2,平均数为x 1若平均数变为x+a那么,每个数也增加了a,则方差为S^2方差不变2若平均数;有n个数,先求平均值Ex,则方差varn=x1Ex^2+x2Ex^2++xnEX^2n方差不仅仅表达了样本偏离均值的程度,更是揭示了样本内部彼此波动的程度,也可以理解为方差代表了样本彼此波动的期望当然。
与本文知识相关的文章:



